Bảng đạo hàm chuẩn và đầy đủ nhất
Các bạn đang tìm kiếm bảng đạo hàm chuẩn và đầy đủ nhất để củng cố kiến thức học tập của mình về phần đạo hàm. Vậy các bạn hãy cùng theo dõi bài viết dưới đây nhé!

Dưới đây là các quy tắc cơ bản, bảng đạo hàm các hàm số cơ bản, đạo hàm cấp cao, đạo hàm của phân thức hữu tỉ, đạo hàm các hàm lượng giác chính xác và đầy đủ nhất.
Quy tắc cơ bản của đạo hàm
- Quy tắc cơ bản
\({\left( c \right)^\prime } = 0\) (với c là hằng số)
\({\left( {uv} \right)^\prime } = {\left( u \right)^\prime }v + {\left( v \right)^\prime }u\)
\({\left( {cu} \right)^\prime } = c.{\left( u \right)^\prime }\)
\({\left( {uv{\rm{w}}} \right)^\prime } = u'v{\rm{w}} + uv'{\rm{w}} + uvw'\)
\({\left( {u \pm v} \right)^\prime } = {\left( u \right)^\prime } \pm {\left( v \right)^\prime }\) (đạo hàm của một tổng bằng tổng các đạo hàm)
\({\left( {\frac{u}{v}} \right)^\prime } = \frac{{{{\left( u \right)}^\prime }v - {{\left( v \right)}^\prime }u}}{{{v^2}}}\)
\({\left( {{x^n}} \right)^\prime } = n.{x^{n - 1}}\) (với n là hằng số tự nhiên)
- Quy tắc đạo hàm của hàm số hợp
Nếu y = y(u(x)) thì \(y'\left( x \right) = y'\left( u \right).u'\left( x \right)\)
Bảng đạo hàm của các hàm số cơ bản
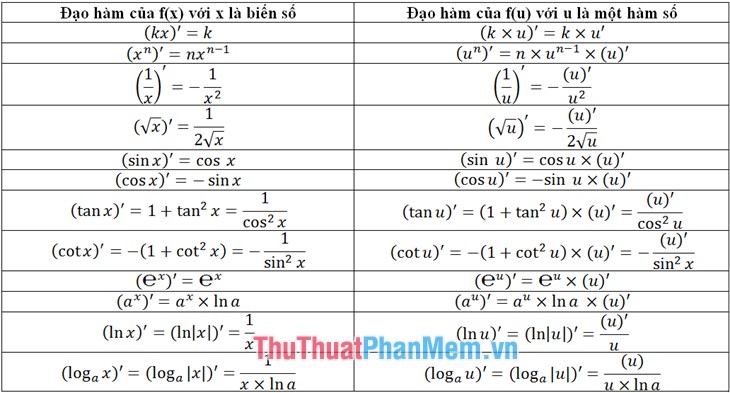
Đạo hàm của một số phân thức hữu tỉ thường gặp

Đạo hàm cấp cao

Đạo hàm các hàm lượng giác và các hàm lượng giác ngược

Trên đây là tổng hợp các công thức đạo hàm chuẩn và đầy đủ nhất dành cho các bạn. Hi vọng các bạn sẽ có thêm những kiến thức hay về phần đạo hàm để củng cố kiến thức toán học cho mình. Chúc các bạn thành công!