Cách tính đường cao tam giác đều

Các bạn đang cần phải tính đường cao tam giác đều, mà các bạn lại không nhớ công thức và cách tính đường cao tam giác đều. Vậy mời các bạn hãy cùng tham khảo bài viết dưới đây để biết công thức và cách tính đường cao tam giác đều.

Dưới đây là cách tính đường cao trong tam giác đều, mời các bạn cùng theo dõi.

Trong hình học, tam giác đều là tam giác có ba cạnh bằng nhau hoặc tương đương ba góc bằng nhau, và bằng 60°. Nó là một đa giác đều với số cạnh bằng 3.

Đường cao của tam giác là đoạn vuông góc kẻ từ một đỉnh đến cạnh đối diện. Cạnh đối diện này được gọi là đáy ứng với đường cao. Độ dài của đường cao là khoảng cách giữa đỉnh và đáy. Mỗi tam giác có 3 đường cao.

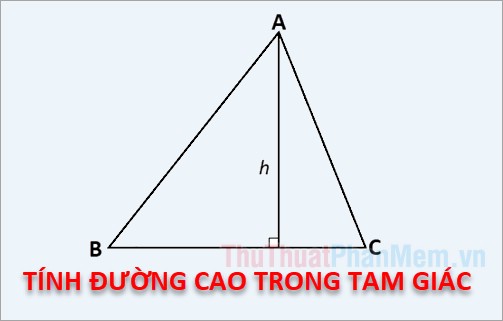
Đường cao trong tam giác đều chính là đường trung trực chia cạnh đối diện thành 2 phần bằng nhau. Một đường cao trong tam giác đều chia tam giác đều thành 2 tam giác vuông bằng nhau.

Giả sử tam giác đều ABC có độ dài cạnh bằng a như hình vẽ

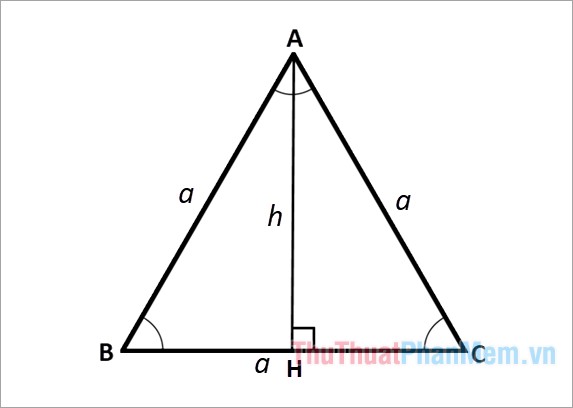
Trong đó: h là đường cao tam giác đều; a là chiều dài cạnh tam giác đều.

Chứng minh công thức

Theo tính chất tam giác đều thì đường cao trong tam giác đều chính là đường trung tuyến vì vậy \(BH = HC = \frac{a}{2}\)

Để tính đường cao trong tam giác đều các bạn áp dụng định lý Pytago trong tam giác vuông ABH: \(A{B^2} = A{H^2} + B{H^2}\)

\( \Rightarrow A{H^2} = A{B^2} - B{H^2}\)

Hay \({h^2} = {a^2} - {\left( {\frac{a}{2}} \right)^2} = {a^2} - \frac{{{a^2}}}{4} = \frac{{4{a^2} - {a^2}}}{4} = \frac{{3{a^2}}}{4}\)

\( \Rightarrow h = \sqrt {\frac{{3{a^2}}}{4}} = a\frac{{\sqrt 3 }}{2}\)

Như vậy bài viết đã chia sẻ đến các bạn cách tính đường cao trong tam giác đều, các bạn chỉ cần sử dụng định lý Pytago là có thể dễ dàng tính được đường cao. Hi vọng bài viết này sẽ giúp cho các bạn dễ hiểu và dễ ghi nhớ cách tính đường cao tam giác đều. Chúc các bạn thành công!