Cách tính thể tích chỏm cầu và ví dụ minh họa
Hình tròn, hình cầu thì đã quá quen thuộc rồi, trong bài này chúng ta cùng tìm hiểu về một dạng hình đặc biệt hơn đó là hình chỏm cầu và cách tính thể tích của chỏm cầu.
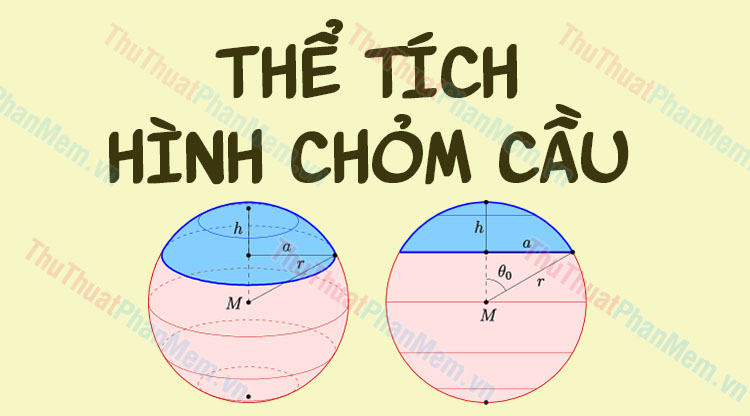
Hình chỏm cầu, hay còn được gọi là hình vòm cầu là một phần của hình cầu bị cắt bởi mặt phẳng. Trường hợp mặt phẳng đi qua tâm hình cầu thì chỏm cầu lúc này chính là hình bán cầu.
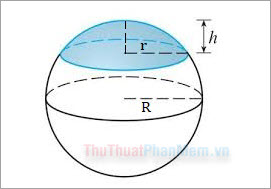
Công thức tính thể tích hình chỏm cầu:
\(V = \pi {h^2}(R - \frac{h}{3}) = \frac{{\pi h}}{6}(3{r^2} + {h^2})\)
Công thức tính diện tích bề mặt hình chỏm cầu:
\({S_{xq}} = 2\pi Rh = \pi ({r^2} + {h^2})\)
Với R: bán kính hình cầu
r: bán kính đường tròn mặt cắt của chỏm cầu
h: chiều cao của chỏm cầu
Ví dụ 1: Cho hình cầu có hình chỏm cầu như hình với chiều cao h = 2cm, bán kính đường tròn mặt cắt chỏm cầu r = 4cm. Tính thể tích chỏm cầu.
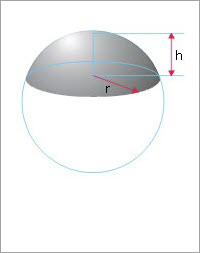
Thể tích chỏm cầu \(V = \frac{{\pi h}}{6}(3{r^2} + {h^2}) = \frac{{2\pi }}{6}(48 + 4) = 54.42(c{m^3})\)
Ví dụ 2: Cho 2 mặt cầu có cùng bán kính R = 5cm với tâm O1 thuộc đường tròn S2 và tâm O2 thuộc đường tròn S1. Tính phần thể tích chung của hai hình cầu này.
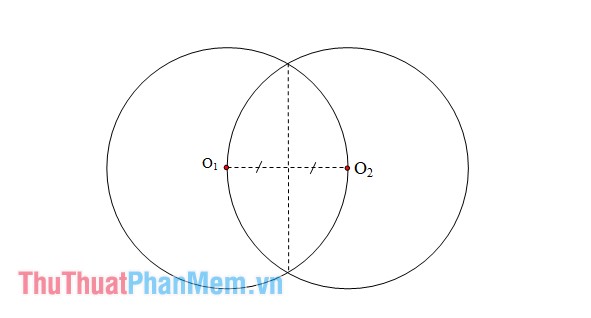
Có thể thấy phần thể tích chung của hai mặt cầu chính là thể tích của 2 chỏm cầu bằng nhau với cùng chiều cao \(h = \frac{R}{2} = \frac{5}{2} = 2.5(cm)\)
=> Thể tích chung của hai mặt cầu là:
\({V_{chung}} = 2x[\pi {h^2}(R - \frac{h}{3}){\rm{]}} = 2x[\pi {2.5^2}{\rm{(5 - }}\frac{5}{6}{\rm{)] = 163}}{\rm{.54(c}}{{\rm{m}}^3})\)
Xosomienbaczone.com đã khái quát xong về hình chỏm cầu và cách tình thể tích hình chỏm cầu kèm ví dụ. Hi vọng qua bài viết này các bạn sẽ có nhiều kiến thức hơn về hình học!