Công thức thể tích khối trụ tròn xoay & Ví dụ
Mục lục nội dung
Thể tích khối trụ tròn xoay là phần kiến thức quan trọng nằm trong chương trình học tập và trong các bài thi cũng không thể thiếu những bài tập tính thể tích khối trụ tròn xoay. Không chỉ vậy trong nhiều lĩnh vực ngoài thực tế, tính thể tích khối trụ tròn xoay cũng là một bài toán hay gặp. Để giúp bạn hiểu rõ hơn về khối trụ tròn xoay cũng như nắm rõ được công thức thể tích khối trụ tròn xoay. Dưới đây Xosomienbaczone.com chia sẻ với bạn công thức thể tích khối trụ tròn xoay & Ví dụ, mời bạn cùng tham khảo nhé.

1. Khối trụ tròn xoay là gì
Khi quay một hình phẳng quanh một trục cố định sẽ được một khối tròn xoay. Hình trụ là hình tròn xoay được sinh ra bởi bốn cạnh của hình chữ nhật khi quay quanh trục cố định.
Khối trụ tròn xoay là hình trụ và phần bên trong của hình trụ đó. Thể tích khối trụ tròn xoay chính là khoảng không gian mà hình trụ chiếm trong không gian.

Một số đặc điểm chính của khối trụ tròn xoay:
- Đáy của khối trụ là hình tròn, đường tròn này sẽ là mặt bên của khối trụ khi nó được quay quanh trục
- Trục của khối trụ là đường thẳng đi qua trung tâm của đáy và là trục quay của hình tròn khi tạo khối trụ tròn xoay
- Mặt bên của khối trụ là các hình tròn song song với đáy có cùng trung tâm với đáy, các mặt bên khối trụ tạo thành bề mặt cong của khối trụ tròn xoay
- Chiều cao của khối trụ tròn xoay là khoảng cách từ mặt đáy đến mặt đỉnh của khối trụ
2. Công thức thể tích khối trụ tròn xoay
Để tính thể tích của khối trụ tròn xoay cần dựa trên diện tích của hình tròn đáy và chiều cao của khối trụ. Cụ thể nếu muốn tính thể tích của khối trụ tròn xoay bạn chỉ cần lấy diện tích mặt đáy nhân với chiều cao của khối trụ.
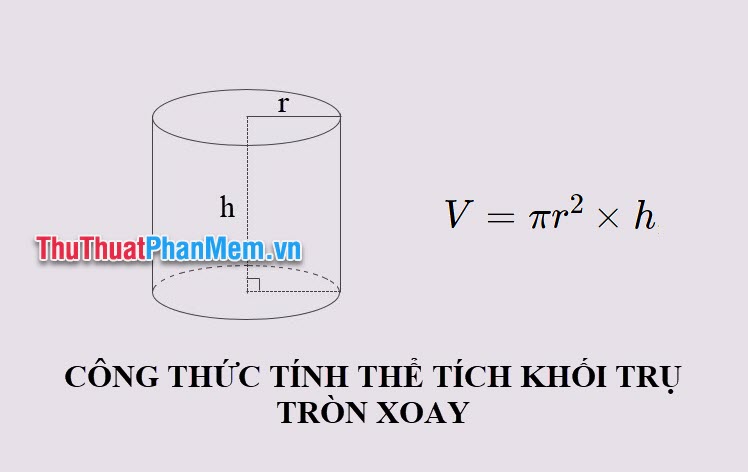
Công thức thể tích khối trụ tròn xoay là: \(V=S_{\mathbb{a}} \times h=\pi r^2 \times h\)
Trong đó:
- V là thể tích của khối trụ tròn xoay
- π là hằng số Pi, có giá trị xấp xỉ 3.14159
- r là bán kính của đường tròn cơ sở của khối trụ (hay chính là bán kính của đường tròn đáy)
- h là chiều cao của khối trụ tròn xoay
3. Ví dụ minh họa
Ví dụ 1: Cho một khối trụ tròn xoay với bán kính r = 5 cm và chiều cao h = 12 cm. Tính thể tích khối trụ tròn xoay đó?
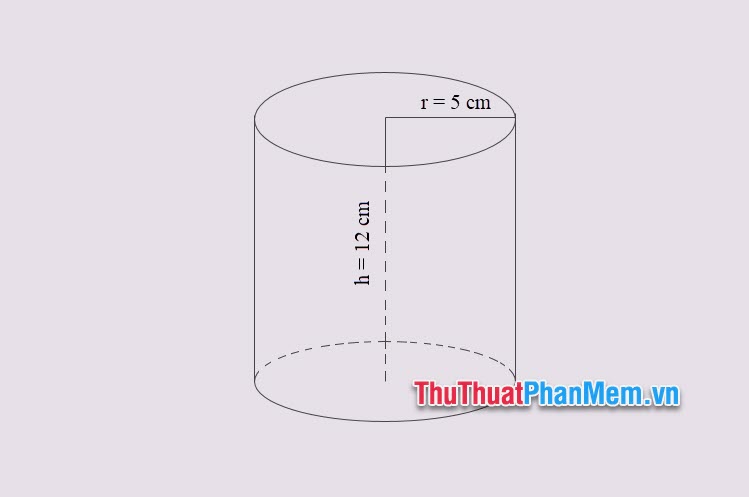
Lời giải
Áp dụng công thức tính thể tích khối trụ tròn xoay \(V=\pi r^2 \times h\), ta có:
\(V=\pi \times 5^2 \times 12=\pi \times 300 \approx 942,478 \mathrm{~cm}^3\)
Vậy thể tích của khối trụ tròn xoay xấp xỉ bằng \(942,478 \mathrm{~cm}^3\)
Ví dụ 2: Cho khối trụ tròn xoay có đáy là hình tròn ngoại tiếp của tam giác đều cạnh a. Biết chiều cao của khối trụ là 3a. Tính thể tích khối trụ tròn xoay đó?
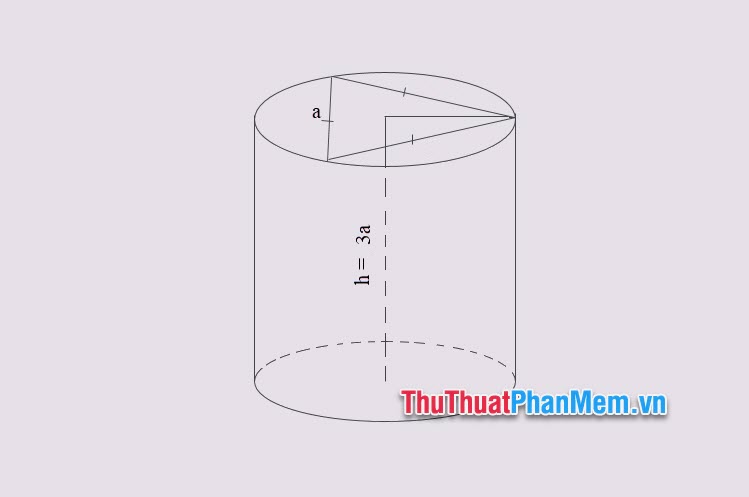
Lời giải
Hình tròn đáy là hình tròn ngoại tiếp của tam giác đều cạnh a, nên theo định lý sin ta có bán kính của hình tròn đó là
\(R=\frac{a}{2 \sin 60^{\circ}}=\frac{a}{2 \frac{\sqrt{3}}{2}}=\frac{a}{\sqrt{3}}=\frac{a \sqrt{3}}{3}\)
Áp dụng công thức tính thể tích khối trụ tròn xoay, ta có:
\(V=\pi r^2 \times h=\pi\left(\frac{a \sqrt{3}}{3}\right)^2 \times 3 a=\pi \times \frac{3 a^2}{9} \times 3 a=\pi a^3\)
Vậy thể tích khối trụ tròn xoay là \(\pi a^3\)
Trên đây, bạn đã cùng Xosomienbaczone.com tìm hiểu về khối trụ tròn xoay, công thức thể tích khối trụ tròn xoay & ví dụ cụ thể. Hi vọng bạn sẽ có thêm được kiến thức hữu ích, nắm rõ hơn về công thức thể tích khối trụ tròn xoay để áp dụng khi gặp những bài toán hay những yêu cầu cần tính thể tích khối trụ tròn xoay. Cảm ơn bạn đã quan tâm và theo dõi bài viết này.