Công thức tính diện tích bề mặt hình cầu & ví dụ minh họa
Mục lục nội dung
Hình cầu là dạng hình học phổ biến không chỉ trong toán học mà còn trong nhiều lĩnh vực và cuộc sống. Nắm chắc được kiến thức về hình cầu, công thức tính diện tích bề mặt hình cầu, bạn có thể nhanh chóng giải những bài toán liên quan đến hình cầu cả trong học tập và cuộc sống hàng ngày. Mời bạn cùng Xosomienbaczone.com tìm hiểu về hình cầu, công thức tính diện tích bề mặt hình cầu & ví dụ minh họa trong bài viết dưới đây nhé.

I. Hình cầu là gì? Diện tích bề mặt hình cầu là gì?
Hình cầu là một vật thể hình tròn ba chiều, với mỗi điểm nằm trên bề mặt của nó đều có khoảng cách đến tâm bằng nhau. Hình cầu được tạo bởi điểm O là tâm, độ dài R là bán kính của hình cầu. Khi quay nửa hình tròn tâm O, bán kính R một vòng quanh đường kính cố định thì được một hình cầu.
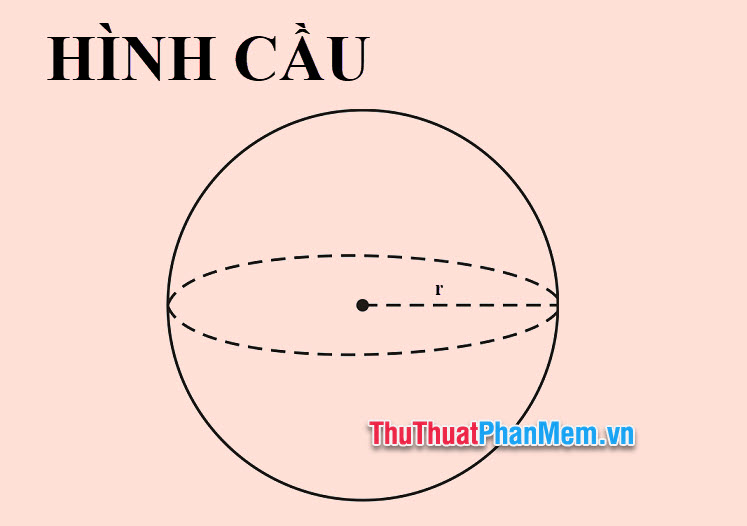
Bán kính hình cầu là khoảng cách từ tâm của một hình cầu đền bề mặt, diện tích bề mặt của một hình cầu chính là tổng diện tích của tất cả các phần của hình cầu. Theo định nghĩa, diện tích mặt cầu được tính bằng 4 lần diện tích hình tròn lớn, hay bằng 4 lần hằng số Pi nhân với bình phương bán kính của hình cầu.
II. Công thức tính diện tích bề mặt hình cầu
Công thức tính diện tích bề mặt hình cầu: \(S=4 \pi r^2=\pi d^2\)
Trong đó:
- S là diện tích bề mặt hình cầu
- \(\pi\) (pi) là một hằng số có giá trị xấp xỉ bằng 3,14159
- \(r\) là bán kính hình cầu (bán kính hình cầu là khoảng cách từ tâm của hình cầu tới bất kỳ điểm nào trên bề mặt của hình cầu)

Đối với một bán cầu (một nửa hình cầu) thì diện tích bề mặt của bán cầu chính là tổng của một nửa diện tích bề mặt của hình cầu cộng với diện tích của đáy bán cầu (chính là hình tròn).
\(S_{\text { bề mặt bán cầu }}=\frac{1}{2} S_{\text { bề mặt hình cầu }}+S_{\text {đáy }}=\frac{1}{2}\left(4 \pi r^2\right)+\pi r^2\)
III. Các dạng bài tập tính diện tích bề mặt hình cầu
1. Tính diện tích bề mặt hình cầu khi biết bán kính
Dạng bài tập này đề bài sẽ cho biết bán kính của hình cầu, yêu cầu tính diện tích bề mặt của hình cầu.
Cách giải: Bạn chỉ cần áp dụng công thức tính diện tích bề mặt hình cầu \(S=4 \pi r^2\) với r là bán kính mà đề bài đã cho trước.

2. Tính diện tích bề mặt hình cầu khi biết đường kính
Dạng bài tập này đề bài sẽ cho biết đường kính của hình cầu, yêu cầu tính diện tích bề mặt của hình cầu.
Cách giải: Bạn chỉ cần tính bán kính hình cầu bằng một nửa đường kính, sau đó áp dụng công thức tính diện tích bề mặt hình cầu.
Hoặc bạn áp dụng công thức tính bán kính hình cầu theo đường kính \(S=\pi d^2\)
3. Tính diện tích bề mặt hình cầu khi biết thể tích
Dạng bài tập này cho biết thể tích hình cầu, yêu cầu tính diện tích bề mặt của hình cầu.
Cách giải: Sử dụng công thức tính thể tích hình cầu để tìm bán kính hình cầu
\(V=\frac{4 \pi r^3}{3}=>r^3=\frac{3 V}{4 \pi}=>r=\sqrt[3]{\frac{3 V}{4 \pi}}\)
Sau khi biết bán kính hình cầu, áp dụng công thức tính diện tích bề mặt hình cầu để tính diện tích.

IV. Ví dụ minh họa
Ví dụ 1: Cho một hình cầu có bán kính nối từ tâm O dài 6cm. Hỏi diện tích bề mặt hình cầu là bao nhiêu.
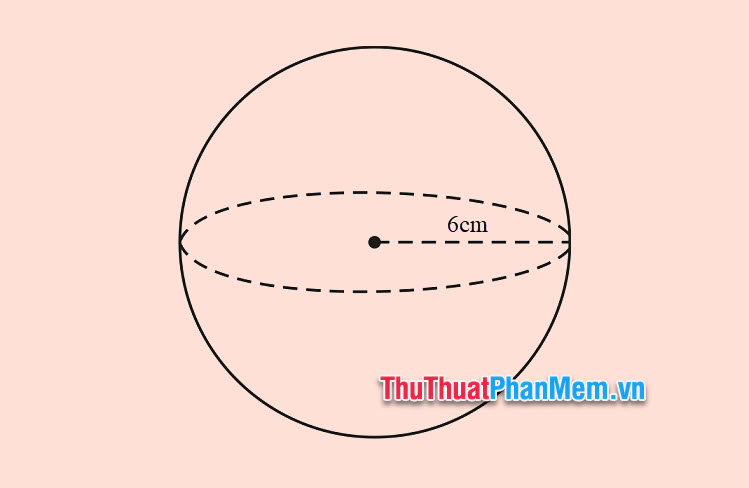
Bài giải
Ta có bán kính hình cầu r = 6 cm, áp dụng công thức tính diện tích bề mặt hình cầu \(S=4 \pi r^2\)
\(S=4 \pi r^2=4 \times \pi \times 6^2=144 \times \pi=452.389 \mathrm{~cm}^2\)
Vậy diện tích bề mặt hình cầu là \(452.389 \mathrm{~cm}^2\).
Ví dụ 2: Cho hình cầu có đường kính 10 cm. Tính diện tích bề mặt hình cầu.
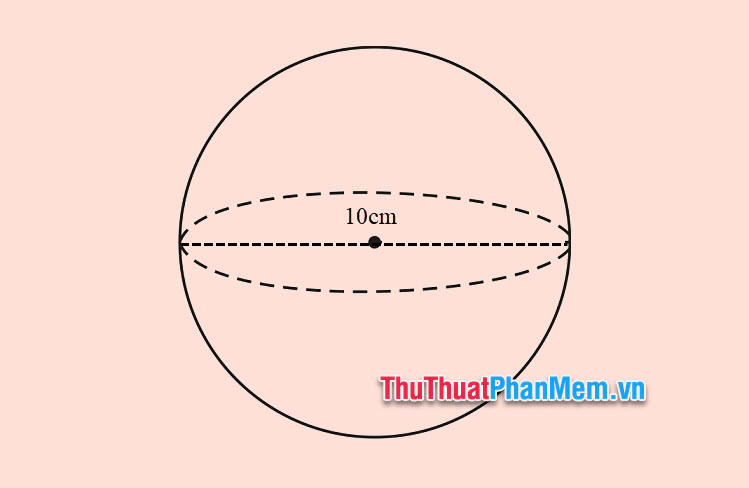
Bài giải
Áp dụng công thức tính diện tích bề mặt hình cầu theo đường kính \(S=\pi d^2\),
Ta có: \(S=\pi d^2=\pi \times 10^2=314.159 \mathrm{~cm}^2\)
Vậy diện tích bề mặt hình cầu là \(314.159 \mathrm{~cm}^2\)
Ví dụ 3: Cho một hình cầu có thể tích là V = 900 cm khối. Tính diện tích bề mặt hình cầu.
Bài giải
Sử dụng công thức tính bán kính hình cầu ta có:
\(r=\sqrt[3]{\frac{3 V}{4 \pi}}=\sqrt[3]{\frac{3 \times 900}{4 \pi} \approx 6,345} \mathrm{~cm}\) cm
Công thức tính diện tích bề mặt hình cầu: \(S=4 \pi r^2=4 \pi \times 6,345^2=505,909 \mathrm{~cm}^2\)
Vậy diện tích bề mặt hình cầu là \(505,909 \mathrm{~cm}^2\)
Như vậy, Xosomienbaczone.com đã chia sẻ với bạn hình cầu là gì, công thức tính diện tích bề mặt hình cầu, các dạng bài tập tính diện tích bề mặt hình cầu và ví dụ minh họa cụ thể. Hi vọng với những kiến thức về hình cầu này, bạn sẽ nắm chắc hơn công thức tính diện tích bề mặt hình cầu, kết hợp với những kiến thức bạn đã học được có thể nhanh chóng giải được những dạng bài tập toán về diện tích hình cầu. Cảm ơn bạn đã quan tâm và theo dõi bài viết này.