Công thức tính đường cao trong tam giác vuông cân & Ví dụ
Mục lục nội dung
Với mỗi dạng tam giác khác nhau thì đường cao trong tam giác sẽ được tính khác nhau. Vậy công thức tính đường cao trong tam giác vuông cân là gì? Mời bạn cùng Xosomienbaczone.com tìm hiểu công thức tính đường cao trong tam giác vuông cân & ví dụ trong bài viết dưới đây nhé.
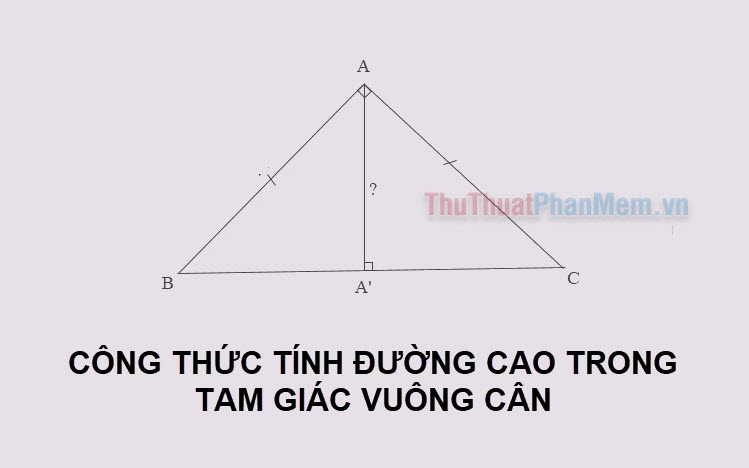
1. Đường cao trong tam giác vuông cân là gì?
Tam giác vuông cân là một loại tam giác có một góc vuông và hai cạnh góc vuông có độ dài bằng nhau, cạnh đối diện với góc vuông là cạnh huyền, hai góc còn lại bằng nhau và đều bằng 45 độ.
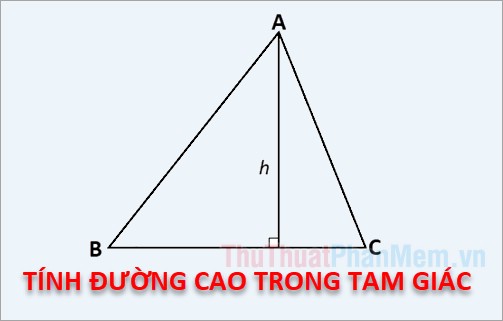
Trong tam giác vuông cân, đường cao chính là đường thẳng vuông góc từ đỉnh góc vuông xuống đường thẳng chứa cạnh đối diện (cạnh huyền) và chia cạnh huyền thành hai đoạn thẳng bằng nhau.

2. Tính chất của đường cao trong tam giác vuông cân
Đường cao trong tam giác vuông cân có các tính chất đặc biệt sau:
- Đường cao trong tam giác vuông cân là đường phân giác của góc vuông: Điểm cắt của đường cao với cạnh huyền của tam giác vuông cân là điểm chính giữa cạnh huyền, nằm trên đường phân giác của góc vuông (chia góc đó thành hai góc có độ lớn bằng nhau)
- Đường cao trong tam giác vuông cân cũng chính là đường trung bình của tam giác vuông cân: Điểm cắt giữa đường cao và cạnh góc vuông là điểm trung điểm của cạnh góc vuông và cạnh huyền
- Đường cao chia tam giác vuông cân thành hai tam giác vuông con bằng nhau: Hai tam giác vuông con này có cạnh huyền chung là đường cao, và các cạnh góc vuông tương ứng cũng là bằng nhau
- Đường cao cũng là đường tâm của tam giác vuông cân: Đường cao cắt nhau tại một điểm duy nhất là tâm của tam giác vuông cân

3. Công thức tính đường cao trong tam giác vuông cân & ví dụ
Cho tam giác ABC vuông cân tại A, \(A A^{\prime}\) là đường cao từ đỉnh A.
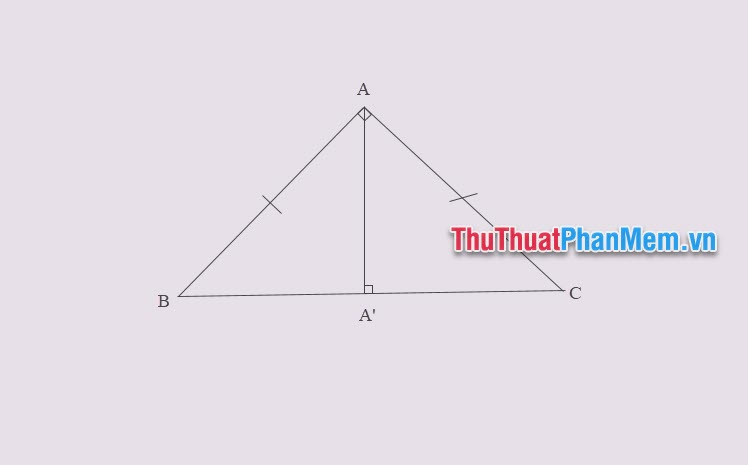
Ta có:
- Đường cao xuất phát từ đỉnh B chính là BA
- Đường cao xuất phát từ đỉnh C chính là CA
- Ta cần tìm độ dài đường cao AA’ xuất phát từ đỉnh A
Xét tam giác vuông AA’B có: \(\widehat{A B A^{\prime}}=45^{\circ}\) do tam giác ABC vuông cân tại A.
Theo tính chất của đường cao trong tam giác vuông cân, đường cao AA’ chia góc vuông \(\widehat{B A C}\) thành 2 góc bằng nhau và bằng 45 độ.
=> Tam giác AA’B vuông cân tại A’
Vậy \(A A^{\prime}=B A^{\prime}=\frac{1}{2} B C\)
Như vậy chiều cao từ đỉnh góc vuông xuống cạnh huyền trong tam giác vuông cân có độ dài bằng \(\frac{1}{2}\) độ dài cạnh huyền.
Ví dụ 1: Cho tam giác ABC vuông cân tại A, độ dài cạnh huyền BC = 6cm. Tính chiều cao \(A A^{\prime}\)
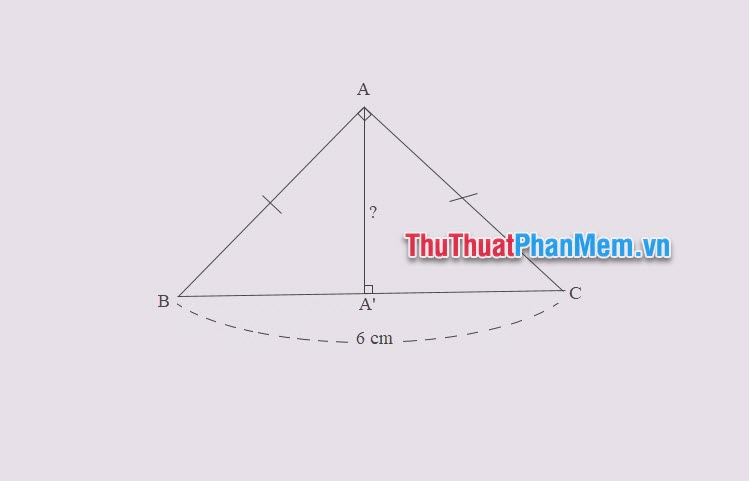
Lời giải
Vì ABC là tam giác vuông cân tại A, nên ta có \(A A^{\prime}=\frac{1}{2} B C\)
Vậy \(A A^{\prime}=\frac{1}{2} \times 6=3 \mathrm{~cm}\)
Ví dụ 2: Cho tam giác vuông cân ABC, độ dài hai cạnh góc vuông AB = AC = 3cm. Tính độ dài đường cao AH.
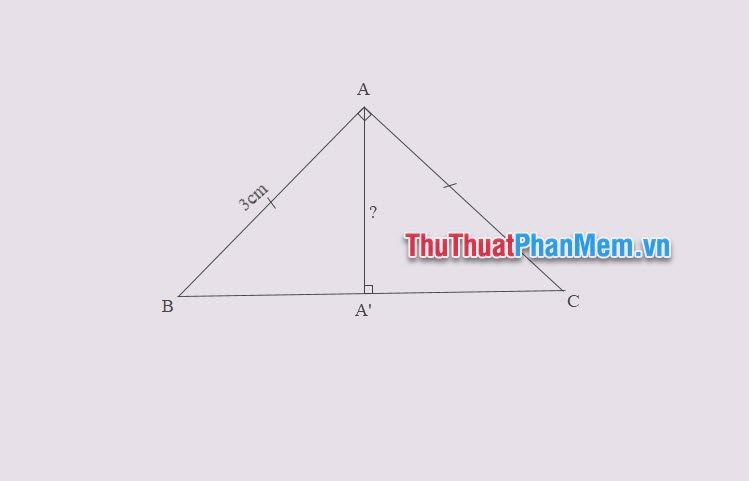
Lời giải
Áp dụng định lý Pytago cho tam giác vuông ABC ta có:
\(B C=\sqrt{A B^2+A C^2}=\sqrt{3^2+3^2}=\sqrt{18}=3 \sqrt{2} \mathrm{~cm}\)
Vậy đường cao \(A H=\frac{1}{2} B C=\frac{1}{2} 3 \sqrt{2}=\frac{3}{2} \sqrt{2} \mathrm{~cm}\)
Như vậy bạn đã cùng Xosomienbaczone.com tìm hiểu về đường cao trong tam giác vuông cân, các tính chất đặc biệt của đường cao trong tam giác vuông cân cũng như công thức tính đường cao trong tam giác vuông cân & ví dụ. Hi vọng bài viết này sẽ mang đến một số kiến thức hữu ích cho bạn trong học tập, cảm ơn bạn đã quan tâm và theo dõi bài viết này.