Công thức tính thể tích hình chóp, cách tính thể tích hình chóp
Các bạn đang tìm kiếm công thức tính thể tích hình chóp, cách tính thể tích hình chóp? Vậy mời các bạn hãy cùng tham khảo bài viết dưới đây để biết công thức và cách tính thể tích hình chóp.
Dưới đây là công thức tính thể tích hình chóp và ví dụ cụ thể về cách tính thể tích hình chóp, mời các bạn cùng theo dõi.
Khái niệm hình chóp
- Hình chóp có mặt đáy là một đa giác và các mặt bên là những tam giác có chung một đỉnh, đỉnh này được gọi là đỉnh của hình chóp.
- Đường thẳng đi qua đỉnh và vuông góc với mặt phẳng đáy được gọi là đường cao của hình chóp.
- Tên gọi của hình chóp dựa vào đa giác đáy: hình chóp có đáy là tam giác gọi là hình chóp tam giác, hình chóp có đáy là tứ giác được gọi là hình chóp tứ giác.
Các khối chóp đặc biệt
1. Hình chóp tứ diện đều
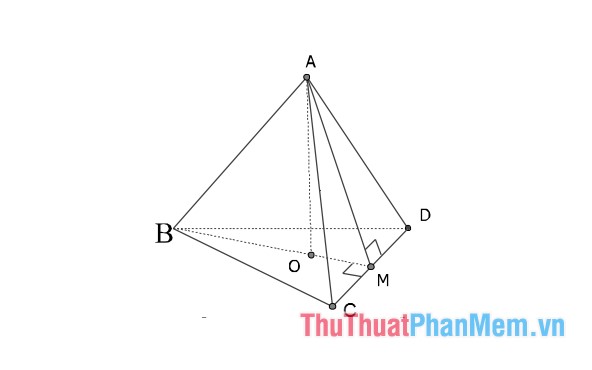
Là hình chóp có tất cả các cạnh bằng nhau, tất cả các mặt đều là các tam giác đều, O là trọng tâm của tam giác đáy và AO ⊥ (BCD).
2. Hình chóp tứ giác đều
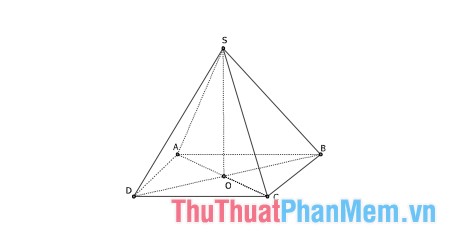
Là hình chóp có tất cả các cạnh bên bằng nhau, đa giác đáy là hình vuông tâm O, SO ⊥ (ABCD).
Công thức tính thể tích hình chóp
Thể tích của hình chóp đều bằng một phần ba diện tích mặt đáy nhân với chiều cao.
\[V = \frac{1}{3}S.h\]
Trong đó:
- V là thể tích hình chóp.
- S là diện tích mặt đáy hình chóp.
- h là chiều cao hình chóp.
- Đơn vị đo thể tích chuẩn là mét khối (\({m^3}\)).
Ví dụ
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh bằng a, cạnh bên SA vuông góc với mặt phẳng đáy và SC tạo với mặt đáy một góc bằng \({60^o}\). Tính thể tích khối chóp S.ABCD.
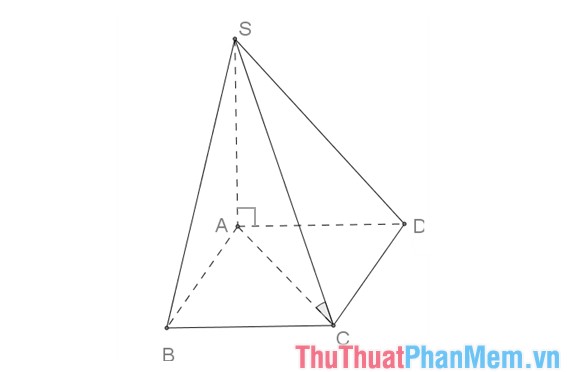
Giải:
Theo công thức tính thể tích \(V = \frac{1}{3}S.h\) thì các bạn cần tính được chiều cao và diện tích mặt đáy.
- Diện tích hình vuông ABCD: \({S_{ABCD}} = a\)
- Tính chiều cao hình chóp:
AC là hình chiếu của SC trên mặt phẳng (ABCD) nên ta có:
\[\left( {SC,\left( {ABCD} \right)} \right) = \left( {SC,AC} \right) = \widehat {SCA} = {45^o}\]
\[AC = a\sqrt 2 ,SA = AC.\tan {60^o} = a\sqrt 6 \]
Sau khi tính được diện tích hình vuông ABCD và chiều cao hình chóp cuối cùng các bạn sẽ tính Thể tích hình chóp:
\[V = \frac{1}{3}.{a^2}.a\sqrt 6 = \frac{{{a^3}\sqrt 3 }}{3}\]
Vậy thể tích hình chóp S.ABCD là \(\frac{{{a^3}\sqrt 3 }}{3}\)
Như vậy trên đây bài viết đã chia sẻ đến các bạn công thức tính thể tích hình chóp và ví dụ cách tính thể tích hình chóp. Hi vọng qua bài viết này các bạn sẽ có thêm kiến thức và hiểu rõ hơn về cách tính thể tích hình chóp. Chúc các bạn thành công!