Hàm BINOM.DIST - Hàm trả về xác suất phân bố nhị thức của thuật ngữ riêng lẻ trong Excel
Bài viết dưới đây giới thiệu tới các bạn hàm BINOM.DIST – 1 trong số những hàm nằm trong nhóm hàm thống kê rất được ưa dùng trong Excel.

Mô tả: Hàm trả về xác suất phân bố nhị thức của thuật ngữ riêng lẻ. Hàm hỗ trợ từ phiên bản Excel 2010.
Cú pháp: BINOM.DIST(number_s,trials,probability_s,cumulative)
Trong đó:
- number_s: số lần thành công trong phép thử, là tham số bắt buộc.
- trials: Số phép thử độc lập, là tham số bắt buộc.
- probability_s: Xác suất thành công của mỗi phép thử, là tham số bắt buộc.
- cumulative: Giá trị logic xác định dạng thức của hàm nếu là giá trị True -> trả về hàm phân bố lũy tích, nếu giá trị False trả về hàm khối xác suất.
Chú ý:
- Nếu number_s và trials không phải là số nguyên chúng bị cắt cụt thành số nguyên.
- Nếu number_s và trials không phải là số -> hàm trả về giá trị lỗi #VALUE!
- Nếu number_s < 0 hoặc number_s > trials -> hàm trả về giá trị lỗi #NUM!
- Nếu probability_s < 0 hoặc probability_s > 1 -> hàm trả về giá trị lỗi #NUM!
- Hàm khối xác suất nhị thức là:
\[b\left( {x,n,p} \right) = \left( {\begin{array}{*{20}{c}}
n\\
x
\end{array}} \right){p^N}{\left( {1 - p} \right)^{n - N}}\]
Trong đó:
\(\left( {\begin{array}{*{20}{c}} n\\ x \end{array}} \right)\): Là COMBIN(n,x).
- Hàm phân bố nhị thức lũy tích là:
\[B\left( {x,n,p} \right) = \sum\limits_{y = 0}^N {b\left( {y,n,p} \right)} \]
Ví dụ:
Tính xác suất của các phép thử với số liệu trong bảng dưới đây:
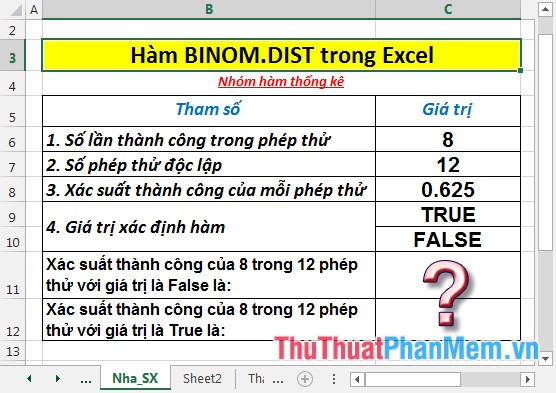
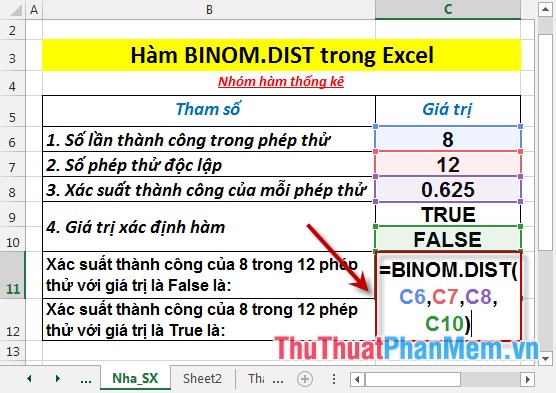
- Tính xác suất thành công của 8 trong 12 phép thử với giá trị là False. Tại ô cần tính nhập công thức: =BINOM.DIST(C6,C7,C8,C10)
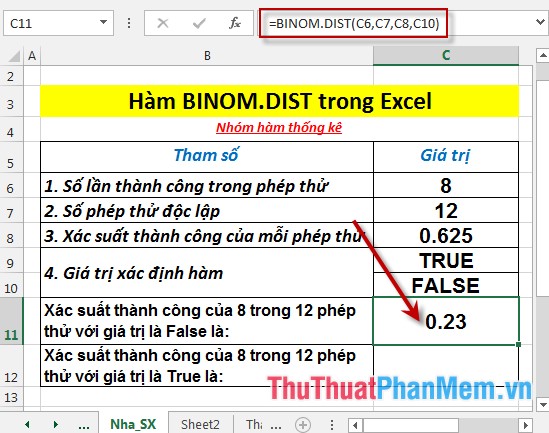
- Nhấn Enter -> xác suất thành công là:
- Tính xác suất thành công của 8 trong 12 phép thử với giá trị là True. Tại ô cần tính nhập công thức: =BINOM.DIST(C6,C7,C8,C9)

- Nhấn Enter -> xác suất thành công là:
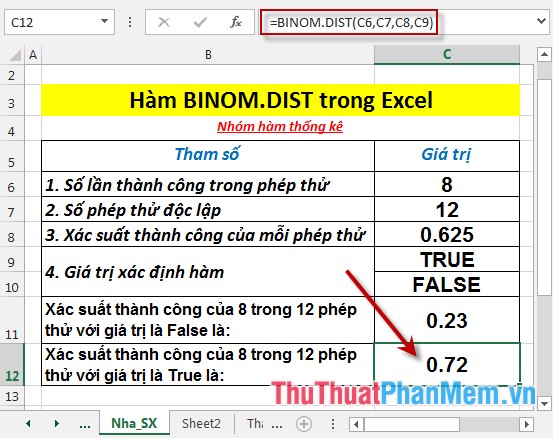
Như vậy với giá trị xác định hàm khác nhau -> hàm trả về kết quả không giống nhau.
Trên đây là hướng dẫn và ví dụ cụ thể khi sử dụng hàm BINOM.DIST trong Excel.
Chúc các bạn thành công!