Hàm CHISQ.TEST - Hàm trả về kiểm định tính độc lập trong Excel
Bài viết dưới đây giới thiệu tới các bạn hàm CHISQ.TEST – 1 trong số những hàm nằm trong nhóm hàm thống kê rất được ưa dùng trong Excel.

Mô tả: Hàm trả về kiểm định tính độc lập. Hàm trả về giá trị từ phân bố (\({\chi ^2}\)) khi bình phương cho việc thống kê và bậc tự do phù hợp. Hàm hỗ trợ từ phiên bản Excel 2010.
Cú pháp: CHISQ.TEST(actual_range,expected_range)
Trong đó:
- actual_range: Phạm vi dữ liệu chứa các quan sát để kiểm thử với giá trị dự kiến.
- expected_range: Phạm vi dữ liệu chứa tỷ lệ của phép nhân tổng hàng và tổng cột với tổng cộng.
Chú ý:
- Nếu actual_range, expected_range có số điểm dữ liệu khác nhau -> hàm trả về giá trị lỗi #N/A.
- Kiểm thử \({\chi ^2}\) tính toán số liệu thống kê \({\chi ^2}\) sử dụng công thức:
\[{\chi ^2} = \sum\limits_{i = 1}^r {\sum\limits_{j = 1}^c {\frac{{{{\left( {{A_{{\rm{ij}}}} - {E_{{\rm{ij}}}}} \right)}^2}}}{{{E_{{\rm{ij}}}}}}} } \]
Trong đó:
+ \({{A_{{\rm{ij}}}}}\): Là tần suất thực tế trong hàng thứ i, cột thứ j
+ \({{E_{{\rm{ij}}}}}\): Là tần suất dự kiến trong hàng thứ i, cột thứ j
+ r: Là số hàng
+ c: Là số cột
- Giá trị dưới của \({\chi ^2}\) là tính độc lập. \({\chi ^2}\) luôn dương hoặc bằng 0 và chỉ bằng 0 khi và chỉ khi \({{A_{{\rm{ij}}}}}\) = \({{E_{{\rm{ij}}}}}\) với mọi i,j.
- Sử dụng hàm CHISQ.TEST thích hợp nhất khi các \({{E_{{\rm{ij}}}}}\) không quá nhỏ
Ví dụ:
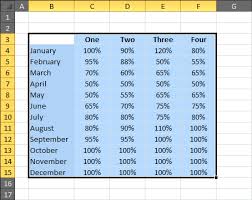
Tính thống kê \({\chi ^2}\) cho kiểm định tính độc lập theo số liệu trong bảng dưới đây:
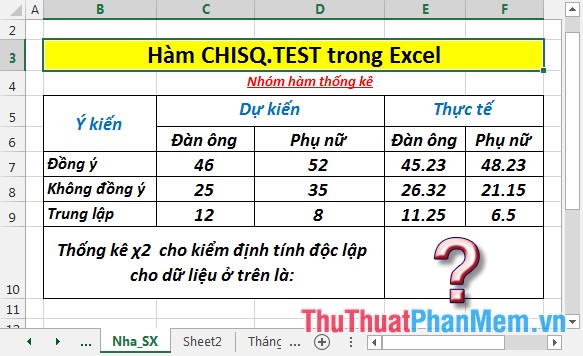
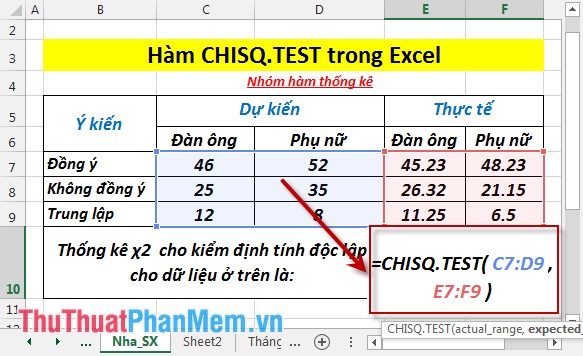
- Tại ô cần tính nhập công thức: =CHISQ.TEST(C7:D9,E7:F9)
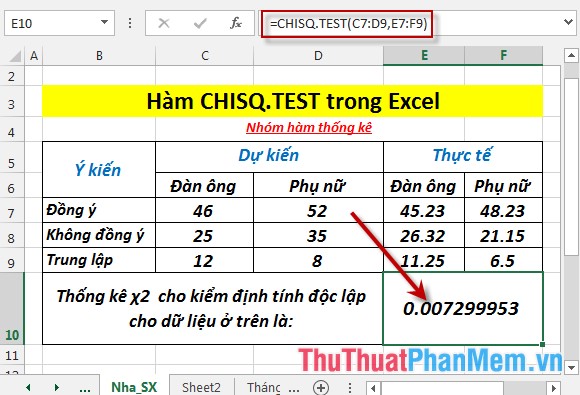
- Nhấn Enter -> thống kê \({\chi ^2}\) cho kiểm định tính độc lập là:
Trên đây là hướng dẫn và một số ví dụ cụ thể khi sử dụng hàm CHISQ.TEST trong Excel.
Chúc các bạn thành công!