Hàm GAMMA.DIST - Hàm trả về phân bố gamma trong Excel
Bài viết dưới đây giới thiệu tới các bạn hàm GAMMA.DIST - 1 trong số những hàm nằm trong nhóm hàm thống kê rất được ưa dùng trong Excel.

Mô tả: Hàm trả về phân bố gamma, sử dụng hàm này để nghiên cứu các biến số phân bố lệch. Hàm hỗ trợ từ phiên bản Excel 2010 trở đi.
Cú pháp: GAMMA.DIST(x,alpha,beta,cumulative)
Trong đó:
- x: Giá trị muốn tính phân bố gamma.
- alpha: Giá trị tham biến tới phân bố.
- beta: Giá Giá trị tham biến tới phân bố, nếu beta = 1 -> hàm trả về phân bố gamma chuẩn.
- cumulative: Giá trị logic xác định dạng thức hàm bao gồm:
+ cumulative = True -> Trả về hàm phân bố lũy tích.
+ cumulative = False-> Trả về hàm mật độ xác suất.
Chú ý:
- Nếu 1 trong các đối sốx, alpha, beta của hàm không phải dạng số -> hàm trả về giá trị lỗi #VALUE!
- Nếu x < 0 hoặc alpha ≤ 0 hoặc beta ≤ 0 -> hàm trả về giá trị lỗi #NUM!
- Phương trình tính hàm mật độ xác suất gamma là:
\[f\left( {x,\alpha } \right) = \frac{1}{{{\beta ^\alpha }\Gamma \left( \alpha \right)}}{x^{\alpha - 1}}{e^{ - \frac{N}{\beta }}}\]
- Phương trình tính hàm mật độ xác suất gamma chuẩn là:
\[f\left( {x,\alpha } \right) = \frac{{{x^{\alpha - 1}}{e^{ - N}}}}{{\Gamma \left( \alpha \right)}}\]
- Khi alpha =1 -> hàm trả về phân bố hàm mũ với:
\[\alpha = \frac{1}{\beta }\]
- Với n nguyên dương, nếu alpha = n/2, beta = 2, cumulative = true -> hàm trả về giá trị (1 - CHISQ.DIST.RT(x)) với n bậc tự do.
- Nếu alpha là số nguyên dương, hàm GAMMA.DIST được gọi là phân bố Erlang.
Ví dụ:
Tìm phân bố và mật độ xác suất GAMMA của giá trị trong bảng dữ liệu dưới đây:
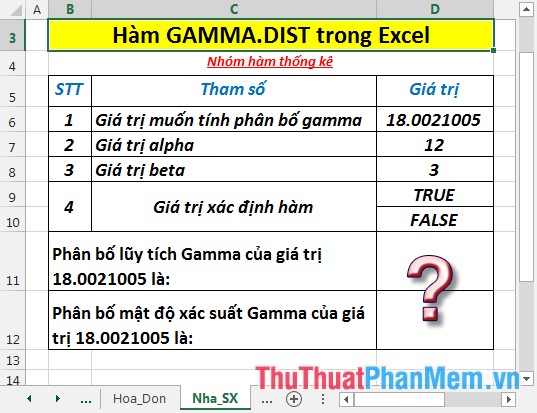
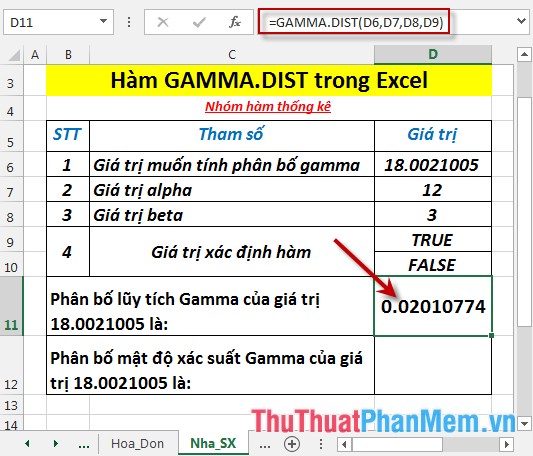
- Tính phân bố lũy tích gamma. Tại ô cần tính nhập công thức: =GAMMA.DIST(D6,D7,D8,D9)

- Nhấn Enter -> phân bố lũy tích GAMMA là:
- Tính phân bố mật độ xác suất gamma. Tại ô cần tính nhập công thức: =GAMMA.DIST(D6,D7,D8,D10)
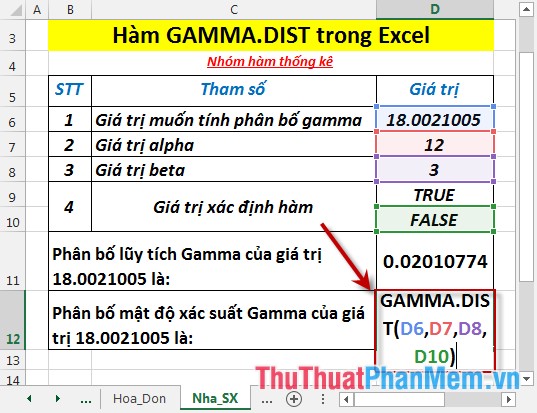
- Nhấn Enter -> mật độ xác suất Gamma là:
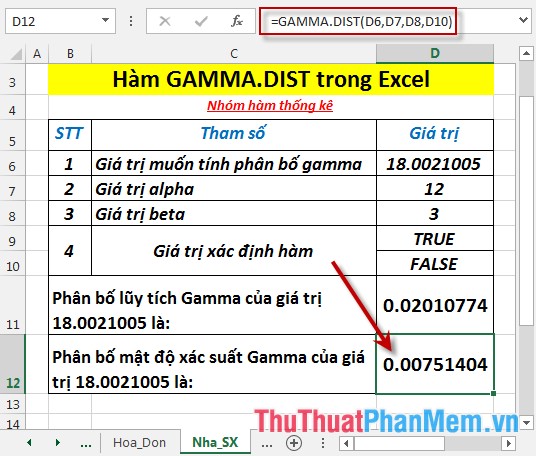
Trên đây là hướng dẫn và một số ví dụ cụ thể khi sử dụng hàm GAMMA.DIST trong Excel.
Chúc các bạn thành công!