Hàm LINEST - Hàm trả về mảng mô tả đường thẳng bằng cách dùng phương pháp bình phương nhỏ nhất trong Excel
Bài viết dưới đây giới thiệu tới các bạn hàm LINEST - 1 trong số những hàm nằm trong nhóm hàm thống kê rất được ưa dùng trong Excel.

Mô tả: Hàm trả về mảng mô tả đường thẳng bằng cách dùng phương pháp bình phương nhỏ nhất.
Cú pháp: LINEST(known_y's, [known_x's], [const], [stats])
Trong đó:
- known_y's: Tập giá trị y đã biết trong quan hệ y = b*m^x, là tham số bắt buộc.
+ Nếu known_y's nằm trong một cột hoặc hàng đơn lẻ -> mỗi cột hoặc hàng của known_y's được hiểu là 1 biến số riêng rẽ.
- known_x's: Tập giá trị x đã biết trong quan hệ y = b*m^x, là tham số tùy chọn.
+ known_x's có thể bao gồm 1 hoặc nhiều tập biến số.
+ Nếu known_x's bị bỏ qua -> nó được giả định là 1 mảng có cùng kích thước với known_y's
- const: Giá trị logic xác định giá trị của hằng số b, là giá trị tùy chọn gồm các giá trị sau:
+ const = True hoặc bỏ qua -> b được tính toán bình thường.
+ const = False hoặc bỏ qua -> b = 1 và m được điều chỉnh sao cho: y = m^x.
- stats: Giá trị logic xác định kiểu thống kê hồi quy bổ sung trả về gồm các giá trị: {mn,mn-1,...,m1,b;sen,sen-1,...,se1,seb;r2,sey;F,df;ssreg,ssresid}.
Chú ý:
- Có thể mô tả bất kì đường thẳng nào bằng độ dốc và giao cắt y:
+ Độ dốc (m):
Để tìm độ dốc của đường thẳng m, lấy hai điểm trên đường thẳng đó, (x1,y1) và (x2,y2) -> độ dốc bằng (y2 - y1)/(x2 - x1).
+ Giao cắt Y (b):
Giao cắt y của một đường thẳng b, là giá trị của y tại điểm mà đường thằng cắt trục y.
Phương trình của đường thẳng là y = mx + b. Có thể tính toán bất kỳ điểm nào trên đường thẳng bằng cách nhập giá trị y hoặc x vào phương trình đó.
- Khi chỉ có một biến độc lập -> sử dụng công thức:
+ Độ dốc:
=INDEX(LINEST(known_y's,known_x's),1)
+ Giao cắt Y:
=INDEX(LINEST(known_y's,known_x's),2)
+ Dùng dấu phẩy phân cách giữa các giá trị trong cùng 1 hàng.
+ Dùng dấu chấm phẩy phân cách giữa các hàng với nhau.
- Khi có một số biến độc lập x -> sử dụng công thức:
\[m = \frac{{\sum {\left( {x - \overline x } \right)\left( {y - \overline y } \right)} }}{{\sum {{{\left( {x - \overline x } \right)}^2}} }}\]
\[b = \overline y - m\overline x \]
Trong đó: x = AVERAGE(known x's) và y = AVERAGE(known_y's).
Ví dụ:
Tính độ dốc và giao cắt y của đường thẳng tương ứng với các giá trị x, y trong bảng dữ liệu dưới đây:
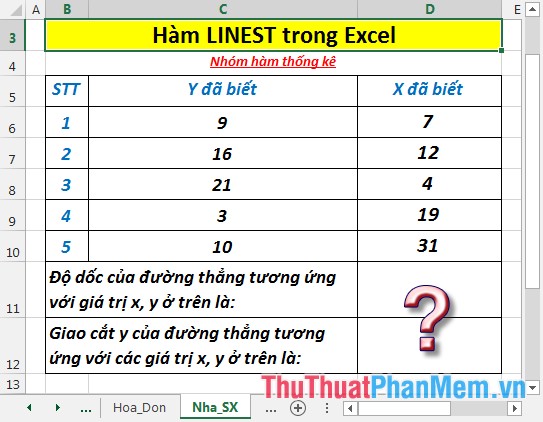
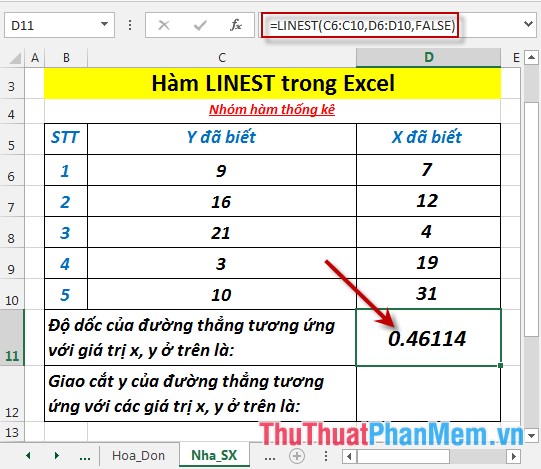
- Tính độ dốc m của đường thẳng tương ứng với các giá trị x, y. Tại ô cần tính nhập công thức: =LINEST(C6:C10,D6:D10,FALSE)

- Nhấn Enter -> độ dốc m của đường thẳng tương ứng với các giá trị x, y là:
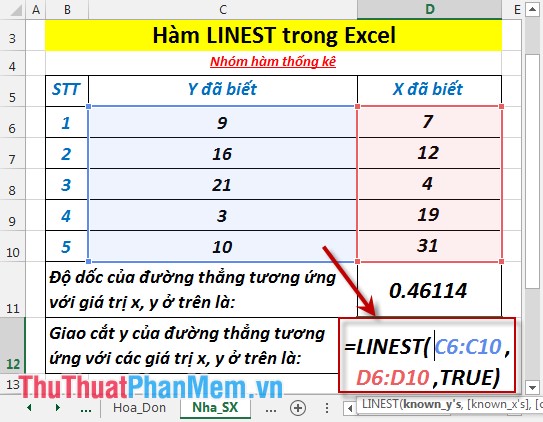
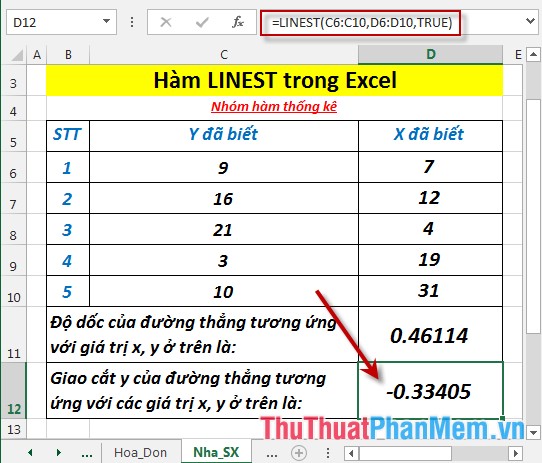
- Tính giao cắt y của đường thẳng tương ứng với các giá trị x, y. Tại ô cần tính nhập công thức: =LINEST(C6:C10,D6:D 10,TRUE)
- Nhấn Enter -> giao cắt y của đường thẳng tương ứng với các giá trị x, y là:
Trên đây là hướng dẫn và một số ví dụ cụ thể khi sử dụng hàm LINEST trong Excel.
Chúc các bạn thành công!