Hàm NORM.DIST - Hàm trả về phân bố chuẩn với độ lệch chuẩn và giá trị trung độ đã xác định trong Excel
Bài viết dưới đây giới thiệu tới các bạn hàm NORM.DIST - 1 trong số những hàm nằm trong nhóm hàm thống kê rất được ưa dùng trong Excel.

Mô tả: Hàm trả về phân bố chuẩn với độ lệch chuẩn và giá trị trung độ đã xác định. Hàm ứng dụng rộng rãi trong thống kê kiểm nghiệm giả thuyết. Hàm hỗ trợ từ phiên bản Excel 2010 trở đi.
Cú pháp: NORM.DIST(x,mean,standard_dev,cumulative)
Trong đó:
- x: Giá trị muốn tính phân bố chuẩn, là tham số bắt buộc.
- mean: Trung độ số học của phân phối, là tham số bắt buộc.
- standard_dev: Độ lệch chuẩn của phân phối, là tham số bắt buộc.
- cumulative: Giá trị logic quyết định dạng thức của hàm, là tham số bắt buộc gồm:
+ cumulative = True -> trả về hàm phân bố lũy tích.
+ cumulative = False -> trả về hàm mật độ xác suất.
Chú ý:
- Nếu mean, standard_dev không phải là số nguyên -> chúng bị cắt cụt thành số nguyên.
- Nếu mean, standard_dev không phải là số -> hàm trả về giá trị lỗi #VALUE!
- Nếu standard_dev ≤ 0 -> hàm trả về giá trị lỗi #NUM!
- Nếu mean = 0, standard_dev = 1 và cumulative = TRUE -> hàm trả về phân bố chuẩn hóa.
- Phương trình của hàm mật độ chuẩn (lũy tích = True) là:
\[f(x;\mu ,\sigma ) = \frac{1}{{\sqrt {2\pi } \sigma }}{e^{ - \left( {\frac{{{{\left( {N - \mu } \right)}^2}}}{{2{\sigma ^2}}}} \right)}}\]
- Nếu cumulative = True -> công thức là tích phân từ âm vô cực tới x.
Ví dụ:
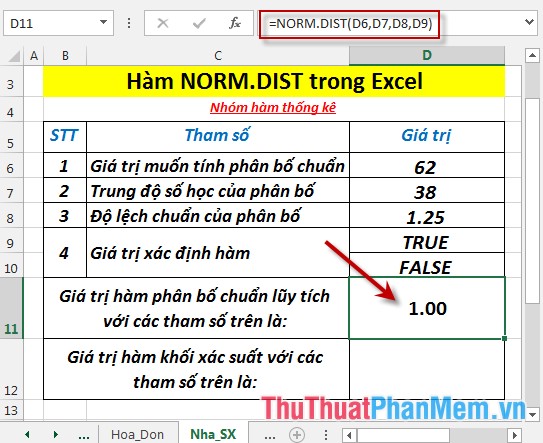
Tìm phân bố chuẩn lũy tích và xác suất với các giá trị trong bảng dữ liệu dưới đây:

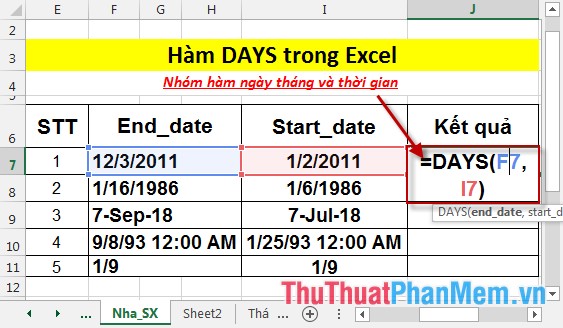
- Tính phân bố chuẩn lũy tích (tương ứng với giá trị True). Tại ô cần tính nhập công thức: =NORM.DIST(D6,D7,D8,D9)

- Nhấn Enter -> phân bố chuẩn lũy tích là:
- Tính giá trị hàm khối xác suất (tương ứng với giá trị False). Tại ô cần tính nhập công thức: =NORM.DIST(D6,D7,D8,D10)

- Nhấn Enter -> giá trị hàm khối xác suất là:
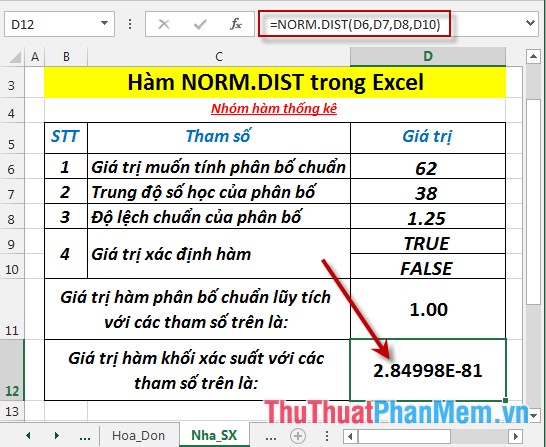
- Có sự sai khá lớn về giá trị giữa hàm phân bố chuẩn lũy tích và phân bố xác suất.
Trên đây là hướng dẫn và một số ví dụ cụ thể khi sử dụng hàm NORM.DIST trong Excel.
Chúc các bạn thành công!