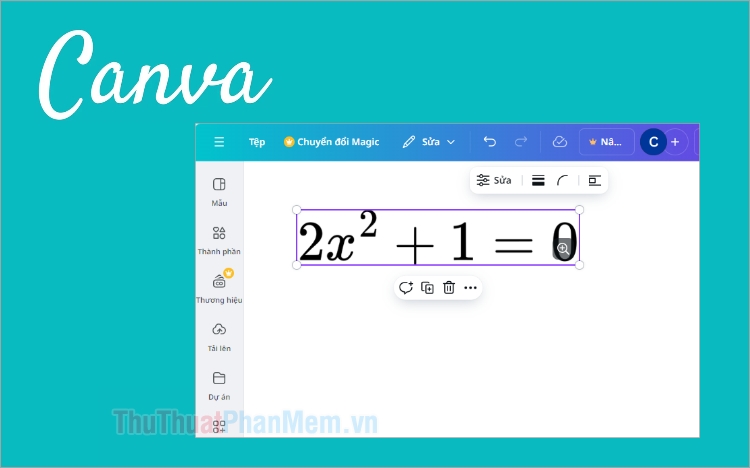
Hàm PERCENTRANK - Hàm trả về thứ hạng của giá trị trong Excel

Trong việc sắp xếp, thống kê dữ liệu bạn rất hay phải xếp thứ hạng cho các đối tượng theo một tiêu chí nào đó. Bài viết dưới đây hướng dẫn chi tiết cách sử dụng Hàm PERCENTRANK tìm thứ hạng của giá trị.

Mô tả: Hàm trả về thứ hạng của 1 giá trị trong tập dữ liệu theo một tiêu chí nào đó. Ví dụ như sử dụng hàm PERCENTRANK để đánh giá kết quả thi của các thí sinh trong các kỳ thi.

Cú pháp: PERCENTRANK(array,x,[significance]).

Trong đó:

- array: Là mảng dữ liệu hoặc phạm vi dữ liệu chứa dữ liệu cần đánh giá, là tham số bắt buộc.

- x: Giá trị muốn xác định thứ hạng, là tham số bắt buộc.

- significance: Tham số tùy chọn dùng để xác định số chữ số trả về của giá trị phần trăm, nếu bỏ qua giá trị mặc định là 3 chữ số sau dấu phẩy (0,xxx).

Chú ý:

- Nếu giá trị mảng trống hàm trả về giá trị lỗi #NUM!

- Nếu significance <1 hàm trả về giá trị lỗi #NUM!

- Trường hợp giá trị x không phù hợp với các giá trị so sánh trong mảng hàm PERCENTRANK thực hiện quá trình nội suy để trả về giá trị thích hợp.

Ví dụ 1:

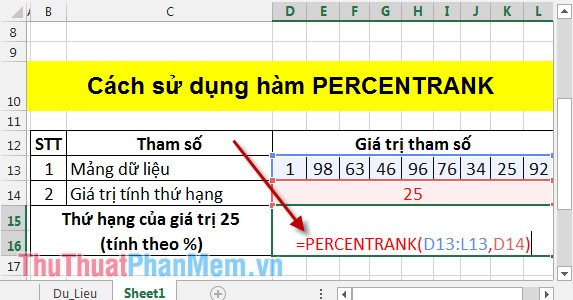
Tìm thứ hạng của giá trị 25 bằng cách sử dụng hàm PERCENTRANK với bảng số liệu sau:

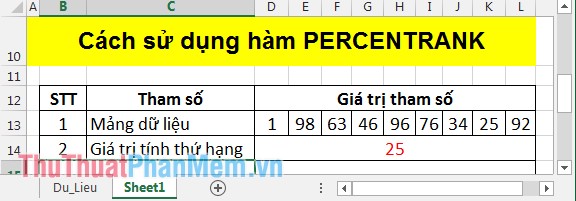
Tại ô cần tính nhập công thức: =PERCENTRANK(D13:L13,D14).

Nhấn Enter kết quả là:

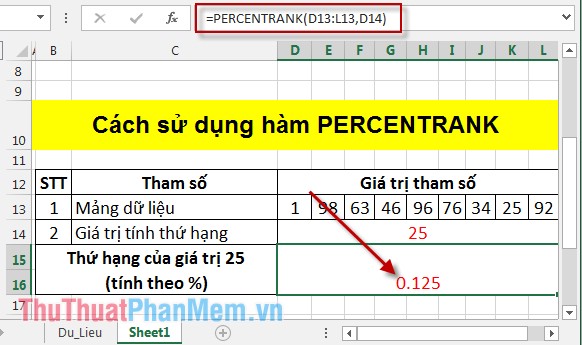
Ở đây giá trị 25 trong mảng dữ liệu có 1 giá trị nhỏ hơn 25 và 7 giá trị lớn hơn 25 => thứ hạng phần trăm của 25 bằng 1/ (1+7)= 0.125.

Ví dụ 2:

Giá trị cần tính thứ hạng phần trăm không có trong mảng dữ liệu.

Ví dụ tìm thứ hạng phần trăm của giá trị 15 trong mảng dữ liệu:

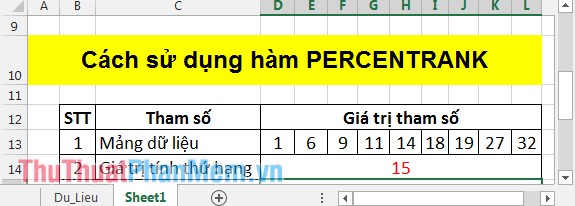
Tại ô cần tính nhập công thức =PERCENTRANK(D13:L13,D14) nhấn Enter kết quả là:

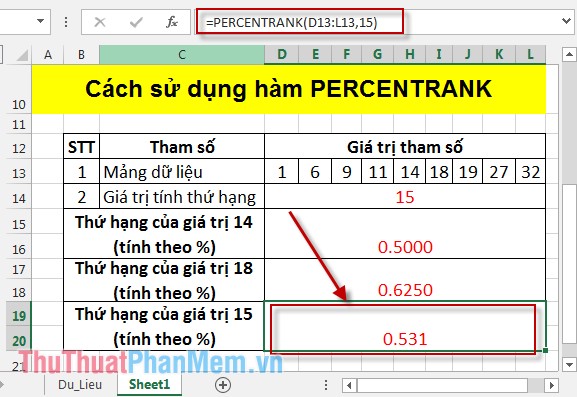
Ở ví dụ này tính PERCENTRANK của 2 giá trị lân cận của 15 là 14 và 18.

Giá trị 15 không nằm trong mảng dữ liệu nên được tính dựa trên 2 lân cận gần nhất của nó dựa vào giá trị PERCENTRANK của 14 và 18:

- PERCENTRANK (14) = 0.5

- PERCENTRANK (18) = 0.625

=> PERCENTRANK (15) = 0.5 + (0.25 *(0.625-0.0.5)) = 0.531

Như vậy nếu giá trị cần tìm thứ hạng phần trăm không có trong mảng dữ liệu hàm thực hiện lấy giá trị lân cận gần nhất và số phần bằng khoảng cách giữa 2 lân cận.

Bài viết trên đây giới thiệu chi tiết cách sử dụng cũng như trường hợp đặc biệt của hàm PERCENTRANK.

Chúc các bạn thành công!