Hàm RSQ - Hàm trả về bình phương của hệ số tương quan mô-men Pearson trong Excel

Bài viết dưới đây giới thiệu tới các bạn hàm RSQ - 1 trong số những hàm nằm trong nhóm hàm thống kê rất được ưa dùng trong Excel.

Mô tả: Hàm trả về bình phương của hệ số tương quan mô-men Pearson thông qua các điểm dữ liệu trong known_y's và known_x's.

Cú pháp: RSQ(known_y's,known_x's)

Trong đó:

- known_y's: Mảng hoặc phạm vi dữ liệu, là tham số bắt buộc.

- known_x's: Mảng hoặc phạm vi điểm dữ liệu, là tham số bắt buộc.

Chú ý:

- Giá trị các đối số phải là số, tên, mảng hoặc tham chiếu có chứa số.

- Giá trị logic và trình bày số kiểu văn bản khi gõ trực tiếp vào danh sách các đối số -> vẫn được tính.

- Các đối số là văn bản hoặc giá trị lỗi không thể chuyển đổi sang kiểu số -> khiến hàm xảy ra lỗi.

- Nếu đối số là mảng tham chiếu có chứa giá trị văn bản hoặc logic -> những giá trị này bị bỏ qua, tuy nhiên giá trị 0 vẫn được tính.

- Nếu known_y's và known_x's trống hoặc có số điểm dữ liệu khác nhau -> hàm trả về giá trị lỗi #N/A.

- Nếu known_y's và known_x's chỉ chứa 1 điểm dữ liệu -> hàm trả về giá trị lỗi #DIV/0.

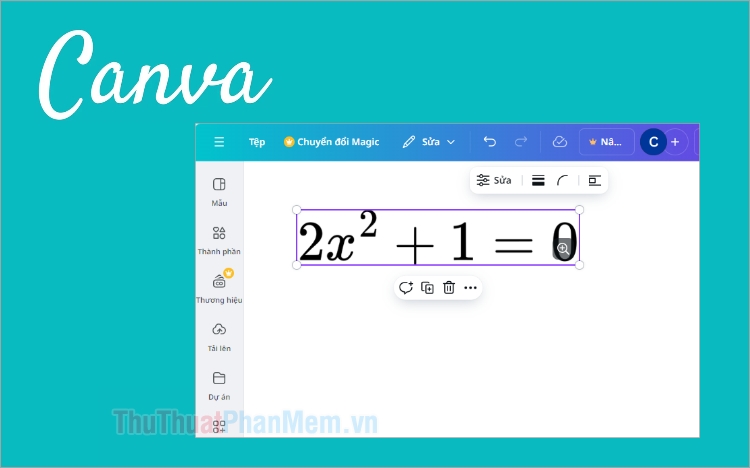
- Phương trình cho hệ số tương quan mô-men tích Pearson, r, là:

\[r = \frac{{\sum {\left( {x - \overline x } \right)\left( {y - \overline y } \right)} }}{{\sqrt {\sum {{{\left( {x - \overline x } \right)}^2}\sum {{{\left( {y - \overline y } \right)}^2}} } } }}\]

Trong đó x và y là các trung độ mẫu AVERAGE(known_x’s) và AVERAGE(known_y’s).

Ví dụ:

Tính bình phương hệ số tương quan mô – men tích Pearson của các giá trị trong bảng dữ liệu dưới đây:

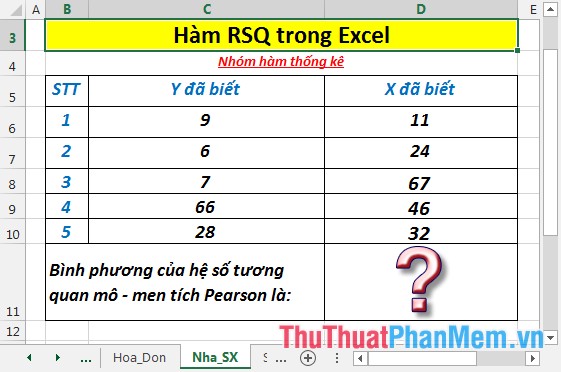
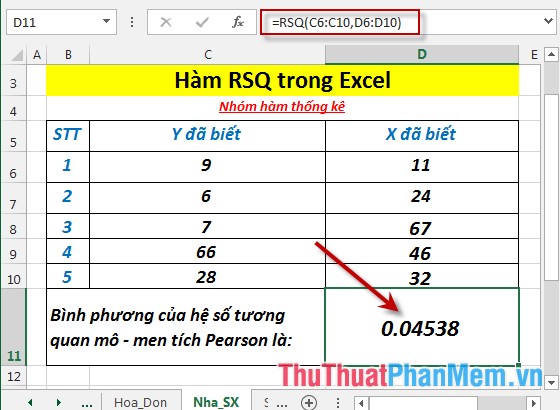
- Tại ô cần tính nhập công thức: =RSQ(C6:C10,D6:D10)

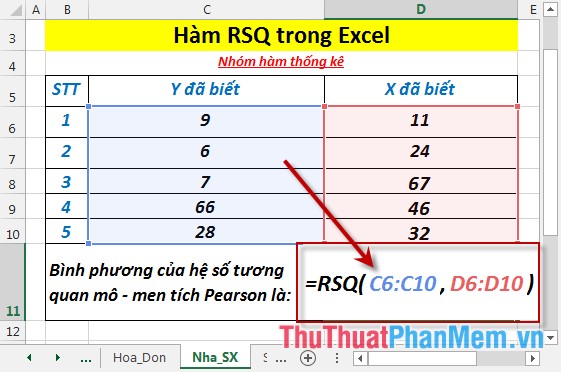
- Nhấn Enter -> bình phương hệ số tương quan mô – men tích Pearson là:

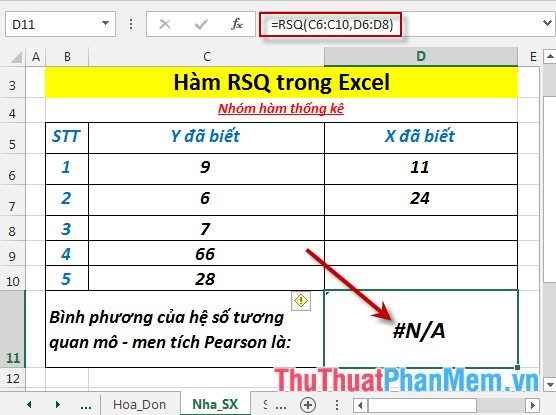
- Trường hợp số phần tử của mảng x và y không bằng nhau -> hàm trả về giá trị lỗi #N/A

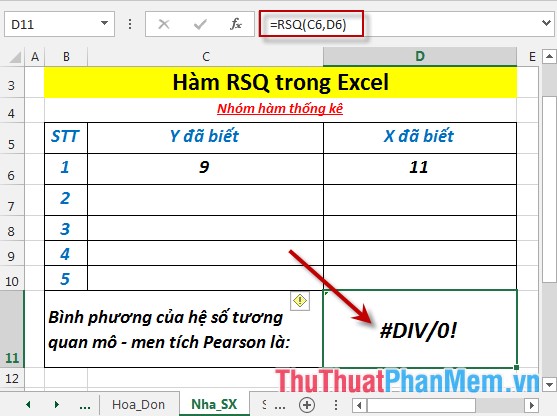
- Trường hợp 2 mảng x, y chỉ có 1 phần tử -> hàm trả về giá trị lỗi #DIV/0.

Trên đây là hướng dẫn và một số ví dụ cụ thể khi sử dụng hàm RSQ trong Excel.

Chúc các bạn thành công!